使用BFS搜索最短路径
前言
广度优先搜索(Breadth First Search),适用于求解关系图中的最短路径问题。 它的适用条件是单点源,无权图的最短路径。
情景设定
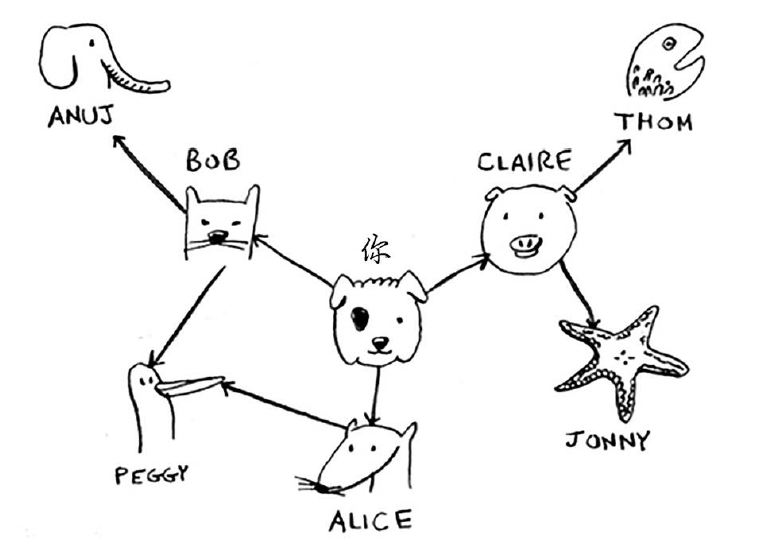
假设你想从朋友关系中寻找到一位芒果经销商(假定姓名结尾字母为m的即为芒果经销商),所以Thom就是我们想要找的芒果经销商。但是你现在还不能联系到Thom,因为你认识的人里只有Bob,Claire和Alice。于是你觉得通过联系你的朋友,请求他继续联系他的朋友来寻找芒果经销商,这里就是Thom。那么,最快联系到Thom的方法是什么呢?
代码实现
首先,上面的关系图可以用下面的多个dict来表达:
graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = []
这里使用了一个临时的方法判断一个人是否是芒果经销商(姓名结尾是m即为芒果经销商):
def person_is_seller(name):
return name[-1] == 'm'
然后使用广度优先搜索的方法:
from collections import deque
def search(name):
print('Searching...')
search_deque = deque()
search_deque += graph[name]
searched = []
while search_deque:
person = search_deque.popleft()
if not person in searched:
if person_is_seller(person):
print(person + " is a mango seller!")
return True
else:
search_deque += graph[person]
searched.append(person)
return False
search('you')
上面的代码告诉了我们朋友关系中是否有芒果经销商,那就是Thom,但是还没有告诉我们如何联系到Thom。那么如何联系到Thom呢?一个解决方法是我们额外创建一个列表parents,在每次节点加入到队列中的时候用来记录它的来源。然后在搜索完毕后利用parents反向从Thom寻找到你!
def search(name):
print('Searching...')
search_deque = deque()
search_deque += graph[name]
searched = []
parents = {}
for p in graph[name]:
if p not in searched:
parents[p] = name
while search_deque:
person = search_deque.popleft()
if not person in searched:
if person_is_seller(person):
print(person + " is a mango seller!")
print('The path from mango seller to you is: ')
prev = person
print(prev)
while True:
prev = parents[prev]
print(prev)
if prev == name:
break
return True, parents
else:
search_deque += graph[person]
searched.append(person)
for p in graph[person]:
if p not in searched:
parents[p] = person
return False, parents
found, parents = search('you')
最后,同样的道理,如果想知道你到Thom最短路径的长度是多少,可是额外创建一个列表dists,在每次节点加入到队列时候记录它们是第几层关系的节点。
def search(name):
print('Searching...')
search_deque = deque()
search_deque += graph[name]
searched = []
parents = {}
dists = {}
dists[name] = 0
for p in graph[name]:
if p not in searched:
parents[p] = name
dists[p] = 1
while search_deque:
person = search_deque.popleft()
if not person in searched:
if person_is_seller(person):
print(person + " is a mango seller!")
print('Distance from %s to mange seller %s is %d' % (name, person, dists[person]))
print('The path from mango seller to you is: ')
prev = person
print(prev)
while True:
prev = parents[prev]
print(prev)
if prev == name:
break
return True, parents, dists
else:
search_deque += graph[person]
searched.append(person)
for p in graph[person]:
if p not in searched:
parents[p] = person
dists[p] = dists[person] + 1
return False, parents, dists
found, parents, dists = search('you')