前言

朴素贝叶斯分类器是一个用来分类的简单可靠的机器学习算法。它主要用来进行文本分类，尤其是对于高维度的训练数据。Naive bayes被称为naive的原因就是因为它假设每一个特征都于其它特征独立。尽管如此它的表现有时能和决策树，神经网络等方法不相上下。应用的场景比如spam filtering， sentimental analysis，或者classifying news articles。

贝叶斯法则

条件概率是指给定一个条件的情况下另一个时间发生的概率。比如令\( A \)表示事件你上学迟到了，令\( B \)表示事件你的闹钟坏了，那么事件\( A \)的发生概率\( P(A) \)和事件\( B \)的发生概率\( P(B) \)都会很小，但是在你闹钟坏掉的情况下迟到的概率，即事件\( B \)的条件下事件\( A \)的发生概率\( P(A|B) \)则会非常大。其中：

\[P(A|B) = \frac{P(A \wedge B)}{P(B)}\]

那么根据上面的公式也可以知道\( A \)和\( B \)共同发生的概率可以计算为：

\(P(A \wedge B) = P(A|B) * P(B)\) 之前是使用\( A \)作为条件，同样的使用\( B \)作为条件也可以得到\( A \)和\( B \)共同发生概率的另一种计算形式：

\[P(A \wedge B) = P(B|A) * P(A)\]

这两种形式的等式的右边也是相等的，从而可以得到著名的贝叶斯公式：

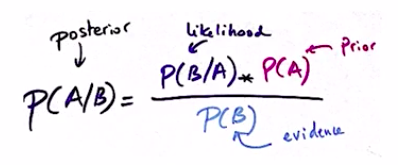
\[P(A|B) = \frac{P(B|A)P(A)}{P(B)}\]

通常\( P(A|B) \)被称为posterior（给定\( B \)时\( A \)的后验概率），\( P(A) \) 称为prior，\( P(B) \)称为evidece，\( P(B|A) \)称为likehood。

如果将样本空间分割为四个相互独立的事件：

  A not A Sum
B P(A and B) P(not A and B) P(B)
Not B P(A and not B) P(not A and not B) P(not B)
  P(A) P(not A)  

在表格边缘的概率称为边缘概率。这里可以得到\( P(B) \)的等式：

\[P(B) = P(A \wedge B) + P(\bar{A} \wedge B)\]

从而得到贝叶斯公式的另一个形式：

\[P(A|B) = \frac{P(B|A)P(A)}{P(B|A)P(A) + P(B|\bar{A})P(\bar{A})}\]

下面举一个具体的例子。加入一个病人得一种罕见病为事件\( A \)， 病人在一家医院被确证为罕见病为事件\( B \)，我们想知道这个病人在被这家医院被确证为罕见病得情况下确实得了罕见病得概率\( P(A|B) \). 同时我们有下面这些概率是可知的：

P(A) = 0.008 P(not A) = 0.992
P(B|A) = 0.98 P(not B|A) = 0.02
P(B| not A) = 0.03 P(not B | not A) = 0.97

这些概率都是容易通过实验进行知道的，那么这是可以计算出在确证为罕见病的情况下确实发病的概率：

\[P(A|B) = \frac{0.98 * 0.008}{0.98 * 0.008 + 0.03 * 0.992} = 0.21\]

只有0.21，这是违背直觉的典型例子，对于罕见病来说即使被准确率很高的医院确诊，真实发病的概率依然很低。

朴素贝叶斯分类器

那么为什么将贝叶斯法则引入到分类任务中？首先回顾一下分类任务的定义：

给定一组训练数据：\( (x_1, y_1), \dots, (x_n, y_n), \quad x_i \in \mathbb{R}^d, \quad y_i \in \mathbb{Y} \)， 分类的任务是希望学习到一个方程：\( f: \mathbb{R}^d \to \mathbb{Y} \)，贝叶斯公式提供了一种使用\( P(y|x) \)的方法来找到这个方程。

目前分类的模型可以分为两大类，一种是Discriminative Algorithm，另一种是Generative Algorithm。贝叶斯分类器是一种典型的Generative方法，逻辑回归是一种典型的Discriminative方法。

  • Discriminative方法的特点是它们都希望找到一个边界来区分正样本和负样本，在预测一个新的样本的时候，是通过边界来检查这个样本属于哪个部分。它们直接预测\( P(y|x) \)
  • Generative方法的思想是是分别建多个模型，分别对应正样本是什么样的，负样本是什么样的。在预测一个新样本时候，去寻找那个模型和当前样本最为匹配。它需要建模\( P(x|y) \)和\( P(y) \)，并使用贝叶斯公式\( P(y|x) = \frac{P(x|y)P(y)}{P(x)} \)来得到结果。

Generative方法在预测时候的思想用公式可以表达为：

\[\mathtt{argmax}_yP(y|x) = \mathtt{argmax}_y \frac{P(x|y)P(y)}{P(x)} \approx \mathtt{argmax}_y P(x|y) P(y)\]

下面详细介绍一下朴素贝叶斯分类的细节。这里分类器的模型设定为训练数据为\( (x_i, y_i) \)，其中\( x_i \)是特征向量，\( y_i \)是离散的标签数据。特征的维度为\( d \)，样本的数量设为\( n \)。比如对于一个文本分类，每个样本表示一个文档，每个特征的维度代表着一个单词在文章中是否出现或者未出现。我们的目标是给定一个训练集，来预测一个新的样本\( x_\text{new} = (a_1, a_2, \dots, a_d) \)的类别\( y_\text{new} \)。这个预测的设定用公式可以写为：

\[y_\text{new} = \mathtt{argmax}_{y \in \mathbb{Y}} P(y| a_1, a_2, \dots, a_d)\]

使用贝叶斯公式，可以进一步转化：

\[\begin{aligned} y_\text{new} &= \mathtt{argmax}_{y \in \mathbb{Y}} P(y| a_1, a_2, \dots, a_d) \\ & = \mathtt{argmax}_{y \in \mathbb{Y}} \frac{P(a_1, a_2, \dots, a_d | y) * P(y)}{P(a_1, a_2, \dots, a_d)} \\ & \approx \mathtt{argmax}_{y \in \mathbb{Y}} P(a_1, a_2, \dots, a_d | y) * P(y) \end{aligned}\]

其中\( P(y) \)可以从统计训练数据中的\( y \)的频率得到。但是\( P(a_1, a_2, \dots, a_d | y) \)不容易得到。\( a_1, a_2, \dots, a_d \)只有在训练集样本量非常巨大的情况下才能得到它们同时发生的条件概率。于是这时朴素贝叶斯分类器的朴素设定便体现出来。朴素贝叶斯分类器有一个非常强的假设是\( a_1, a_2, \dots, a_d \)在\( y \)的条件下的概率相互独立，于是使得\( a_1, a_2, \dots, a_d \)共同发生的概率转化为各自概率的乘积：

\[P(a_1, a_2, \dots, a_d | y) = \prod_j P(a_j | y)\]

而每个事件\( a_j \)的条件概率\( P(a_j|y) \)是容易从一个适量的数据集中获得的。所以我们得到朴素贝叶斯分类器的完整形式：

\[\hat{y} = \mathtt{argmax}_{y \in \mathbb{Y}} P(y) \prod P(a_j | y)\]

其中\( P(y) \)和\( P(a_j|y) \)都容易从训练集中得到。这里总结朴素分类器的步骤：

  • 训练阶段
  1. 计算所有的先验概率\( p(y), \forall y \in \mathbb{Y} \)
  2. 计算所有的似然概率\( P(a_j | y) \quad \forall y \in \mathbb{Y}, \quad \forall a_i \)
  • 预测阶段，对于每一个样本，使用：
\[\hat{y} = \mathtt{argmax}_{y \in \mathbb{Y}} P(y) \prod P(a_j | y)\]

使用Python从头实现朴素贝叶斯分类器

这里的例子是使用Pima Indians Diabetes problem，它包含768例印度糖尿病人的生理数据。每一条记录包含病人的特征比如年龄，怀孕次数等，所有特征都是数字特征，每个特征的单位和范围均有所不同。病人的标签为5年内是否检测到糖尿病发生，用1和0来表示。这些记录的例子比如：（下载)

6,148,72,35,0,33.6,0.627,50,1
1,85,66,29,0,26.6,0.351,31,0

参考上一节的步骤，训练步骤：

  • 我们需要先统计标签的评论得到\( P(y) \):
  • 这里假设每个特征均为一维高斯分布，于是统计不同标签条件下，每个特征的均值\( \mu \)和方差\( \sigma \)得到这个分布，对于新的样本，可以使用这个标签的特征值和对应的高斯概率密度函数得到\( P(a_j | y) \), 其中高斯概率密度函数为：
\[f(x | \mu, \sigma^2) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}}\]

其中\( \mu \) 对应训练集中某一个标签下的那个特征的均值，\( \sigma \)同理。预测阶段对每个测试样本计算：

\[\hat{y} = \mathtt{argmax}_{y \in \mathbb{Y}} P(y) \prod P(a_j | y)\]

整个过程的代码如下：

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split

# Read csv file and split the train and test set
data = pd.read_csv("./pima-indians-diabetes.data.csv", header=None)
X_train, X_test, y_train, y_test = train_test_split(data.iloc[:, :8], data.iloc[:, 8], random_state=2033)
print("Ratio of Train / Test is {}/{}".format(len(X_train), len(X_test)))

# Train phase:
# Compute the distribution of likehood of each sample for each feature in terms of each label.
# Firstly, filter the sample by the class label y.
# Then, calculate the mean and variation of each feature for different labels.
mean, std = {}, {}
for y in [0, 1]:
    mean[y] = X_train[y_train == y].mean(axis=0)
    std[y] = X_train[y_train == y].std(axis=0)
print("Training done")

# Predict phase:
# Covert the value of each sample into the likehood P(a_j | y). Here use the guassian density function. Here convert the value of each sample use guassian density function.
def wrapper(mean, std):
    """wrapper for gaussian density function"""
    def func(x):
        exponent = np.exp(- np.square(x - mean) / (2 * std * std))
        factor = (1 / (np.sqrt(2 * np.pi) * std))
        out = factor * exponent
        return out
    return func

def cal_prob(vector, y):
    """calculat the probability of one sample"""
    prob = 1
    for i, e in enumerate(vector):
        func = wrapper(mean[y][i], std[y][i])
        prob *= func(e)
    return prob

preds = []
for row in range(0, len(X_test)):
    pred = max([0, 1], key=lambda y:cal_prob(X_test.iloc[row], y))
    preds.append(pred)

# Evaluate the accuracy
assert len(y_test) == len(preds), "The count of predictions should equal the test set"
correct_num = sum(pred == target for pred, target in zip(preds, y_test))
acc = correct_num / len(y_test)
print("Accuracy: {:.2f}".format(acc))

使用sklearn的接口实现朴素贝叶斯分类器

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
import seaborn as sns; sns.set(color_codes=True)
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(df, iris.target)
gnb.score(df, iris.target)

扩展

  • m-estimate: 如果\( P(a_j|y) \)都非常小，那么可能导致\( \prod_j P(a_j|y) \)无限接近于0。这时候可以考虑使用m-estimate:

    \[P(a_j | y) = \frac{n_c + m*p}{n_y + m}\]

    其中\( n_y \)是对于类别\( y \)对样本总数，\( n_c \)是类别\( y \)下满足\( x_j = a_j \)对样本数，\( m \)是一个伪采样数量，\( p \)是一个先验概率。例如在一个词汇数量1000点文本分类任务重，如果某单词出现频率太低，可以令\( P(a_j|y) = \frac{n_c + 1}{ n_y + 1000} \)。这里假设每个词汇出现的先验概率均等。

  • Log probability: 针对条件概率过小的另一个方法是将它转换到对数空间。
  • Nominal Attribute: 糖尿病的数据集中都是数字特征，对于类别特征（比如颜色），可以通过统计训练集中某个标签条件下，特征各个类别的频率来得到likehood。
  • Different Density Function: 实现不同分布假设的朴素贝叶斯分类器病讨论这些假设的合理性和它们的关系，比如multinomial, bernoulli or kernel naive bayes。

Reference

Document

Video

Code