前言

Vanilla GAN

2014年Goodfellow提出了一个训练生成模型的方法称为Generative Adversarial Networks(GAN)。在GAN中，我们会构建两个神经网络，第一个网络是常见的分类网络，称为判别器（Discriminator），这个网络可用来对输入的图片进行分类判断：True（这张图片属于训练集）， False（这张图片不存在于训练集）。另一个网络，称为生成器（Generator），将以随机噪声为输入然后将噪声转化为一张图片（一个\(H \times W \times C\)的张量）。生成器的目标是能够生成以假乱真的图片让判别器不能正确分类。

更加正式的，可以将这个生成器\(G\)和判别器\(D\)的交错训练的过程写成：

\[\underset{G}{\text{minimize}}\; \underset{D}{\text{maximize}}\; \mathbb{E}_{x \sim p_\text{data}}\left[\log D(x)\right] + \mathbb{E}_{z \sim p(z)}\left[\log \left(1-D(G(z))\right)\right]\]

这里\(z \sim p_\text{z}\)是随机噪声，\(G(z)\)是适应生成器网络\(G\)生成的图片，\(D(x)\)是判别器网络\(D\)的预测结果。

可以被证明的是在使用optimal discriminator来最小化GAN的目标函数的时候，相当于在最小化训练集数据分布和生成器\(G\)生成样本的JS-devergence。

实际操作中，训练GAN的过程是两步交替执行的：

  1. 通过最大化判别器正确判断的概率来更新判别器\(D\)的参数。
  2. 通过最小化判别器正确判断的概率来更新生成器\(G\)的参数。

但是由于减小梯度消失的问题带来的影响，通常会将第2步的目标函数改为最大化判别器错误判断的概率，这参考自Goodfellow。这个过程更为正式的写法即：

  1. 通过最大化判别器正确判断的概率（正确分类真实样本和生成样本），更新判别器\(D\)的参数：
\[\underset{D}{\text{maximize}}\; \mathbb{E}_{x \sim p_\text{data}}\left[\log D(x)\right] + \mathbb{E}_{z \sim p(z)}\left[\log \left(1-D(G(z))\right)\right]\]
  1. 通过最大化生成其错误判断的概率，更新生成器\(G\)的参数：
\[\underset{G}{\text{maximize}}\; \mathbb{E}_{z \sim p(z)}\left[\log D(G(z))\right]\]

从Vanilla GAN出发：

大量的workshops，papers提出了不同的GAN方法并进行比较，这些方法有的简单有效，有的复杂而且十分难训练，复现论文需要特殊的tricks。而WGAN和WGAN-GP就是两个稳定GAN的训练过程的方法。

GAN不是唯一的生成模型，另一个流行的训练神经网络的生成模型是Variational Autoencoders（参考1，2）

WGAN的问题

Weight Clipping强制实现了在critic模型上， 既满足Lipschitz constraint同时计算Wasserstein距离。

Quote from the research paper: Weight clipping is a clearly terrible way to enforce a Lipschitz constraint. If the clipping parameter is large, then it can take a long time for any weights to reach their limit, thereby making it harder to train the critic till optimality. If the clipping is small, this can easily lead to vanishing gradients when the number of layers is big, or batch normalization is not used (such as in RNNs) … and we stuck with weight clipping due to its simplicity and already good performance.

Weight clipping是一个简单的方法，但是同时也带来了问题，比如超参数$c$的选择。

\[w \gets clip(w, -c, c)\]

模型的性能对于这个超参数非常敏感，在下面的图中，当batch normalization去掉的时候，discriminator随着$c$从0.001到0.1，表现出从diminishing graidents到exploding gradients。

clip

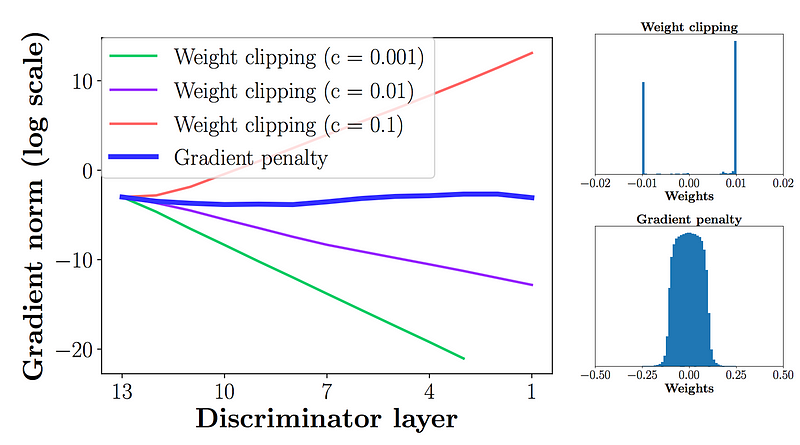
另一个问题是weight clipping减小的模型的capacity限制了它对于复杂函数的表达能力。在下面的实验中，第一行是WGAN的结果，第二行是WGAN-GP的结果。由于capacity的限制，WGAN在根据给出的信息(橙色的点)创建复杂边界的时候，能力逊色与WGAN-GP。

boundary

Wasserstein GAN with gradient penalty (WGAN-GP）

一个可微分函数$f$是1-Lipschtiz，当且仅当它的gradients的范数在每个地方为1。

所以weight clipping的替代方案是给原来的WGAN损失函数增加一个正则项，当梯度范数偏离1的时候对模型进行惩罚。

\[L = \mathbb{E}_{\tilde{x}\sim \mathbb{P}_g} [D(\tilde{x})] - \mathbb{E}_{x\sim \mathbb{P}_r} [D(x)] + \lambda\mathbb{E}_{\hat{x}\sim\mathbb{P}_{\hat{x}}}[(||\bigtriangledown_{\hat{x}}D(\hat{x})||_2 - 1)^2]\]

这里，\(\lambda\)设置为10，用来计算gradient norm的点\(\hat{x}\)是从\(\mathbb{P}_g\)和\(\mathbb{P}_r\)之间采样的任意点。

\[\hat{x} = t \tilde{x} + (1-t)x \quad \text{with} \quad 0 \le t \le 1\]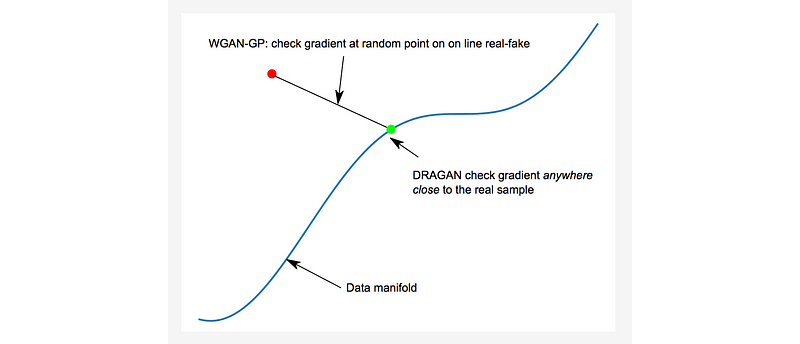

hatx

对于这个critic(discriminator)，不要使用batch normalization。Batch normalization会同一个batch中的samples建立correlation。这在实验中证明会影响gradient penalty的作用。

实验中发现虽然WGAN-GP相对于WGAN表现出更好的图片质量和收敛，但是DCGAN的图片质量和收敛却更快。但是WGAN-GP的inception score在收敛后更加稳定。

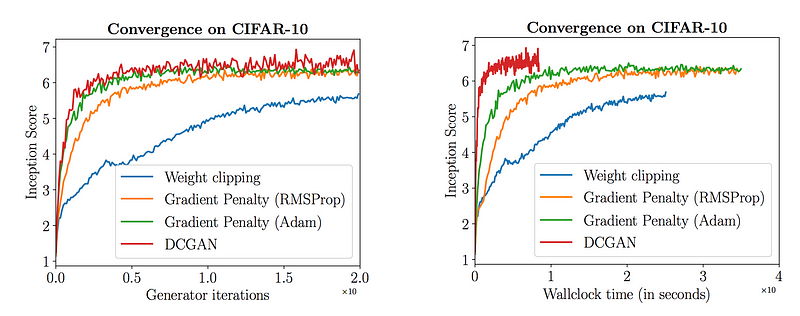
inception score

所以WGAN-GP的优势是什么？它的主要优势是它的收敛性。它使得训练更加稳定也更建简单。因此我们可以使用更复杂的模型比如ResNet作为generator和discriminator。

Reference