Attention Mechanism
前言
RNN可以用来建模words之间的条件概率:
\[P(w_1 w_2 \dots w_n) \approx \prod_i P(w_i | w_{i-k} \dots w_{i-1})\]传统的Seq2Seq模型对输入序列X缺乏区分度,因此,2015年,Kyunghyun Cho等人在论文《Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation》中,引入了Attention Mechanism来解决这个问题,他们提出的模型结构如图:
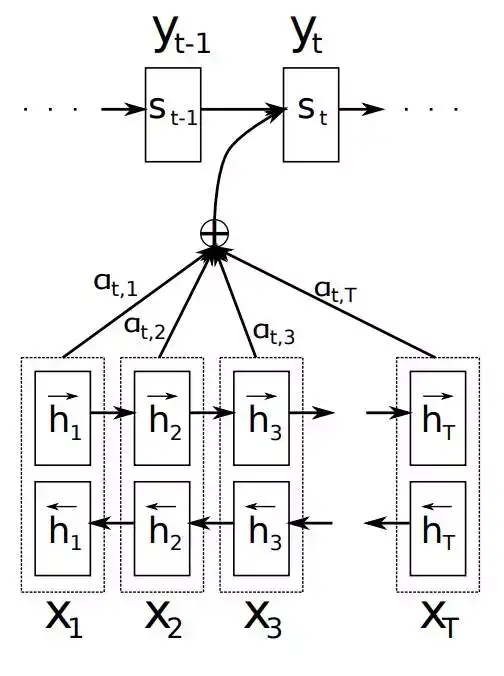
该模型定义了一个条件概率:
\[p(y_i | y_1, \dots, y_{i-1}, X) = g(y_{i-1}, s_i, c_i)\]其中\(s_i\)是decoder中RNN在\(i\)时刻的隐状态,其计算公式为:
\[s_i = f(s_{i-1}, y_{i-1}, ci)\]这里的\(c_i\)是context vector,它是一个权重加和之后的值,具体表达公式如下:
\[c_i = \sum_{j=1}^{T_x} \alpha_{ij}h_j\]这里\(\alpha_{ij}\)表示encoder端第\(j\)个词与decoder端第\(i\)个词之间的权重,即源端第\(j\)个词对目标端第\(i\)个词的影响程度。计算\(\alpha_{ij}\)的公式如下:
\[\alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{k=1}^{T_x}\exp(e_{ik})}\] \[e_{ij} = a(s_{i-1}, h_j)\]\(e_{ij}\)表示一个对齐模型,用于衡量decoder端生成位置\(i\)的词时候,有多少程度收到encoder端\(j\)位置词的影响。对齐模型的计算方法有多种:
\[score(h_t, \bar{h}_s) = \begin{cases} h_t^T \bar{h_s} & \text{dot} \\ h_t^T W_\alpha \bar{h}_s & \text{general} \\ v_\alpha^T \tanh (W_\alpha [h_t; \bar{h}_s]) & \text{concat}\\ \end{cases}\]