决策树简介（原理以及代码从零实现）

决策树是一个强大的预测模型，它使用树结构在每个节点对数据进行简单的判断，通过多个节点连续的判断在叶子节点做出预测，由于使用这样的判断过程，它的预测结果非常易于解释。决策树既适用于分类任务也适用于回归任务。决策树还是其它集成学习方法的基础，比如bagging，random forests，gradient boosting等，这样方法能够使用简单的决策树创建更加强大的模型。本篇博客会介绍什么是决策树，如何创建一个决策树，创建决策树时用到的基尼系数，以及它们的代码实现。

Tree vector created by brgfx - www.freepik.com

简介

本博客介绍一下如何使用Python从头实现一个CART树。CART树是一个二叉树结构（binary tree），和基础的树结构一样每个节点包含0到2个分支连接到其它节点，包含0个分支的节点即使叶子节点。每个节点包含一个选择条件，这个条件决定了输入变量流入哪个分支，流入的分支即为预测的结果。

什么是决策树

一个最简单的决策是为如图的二叉树结构，它的节点为一个判断条件比如你的提问是否大于38度，根据判断条件的结果会流向不同的分支，即如果你的体温大于38度，那么判断你发烧了你需要进行治疗，否则你不需要进行相关的治疗。

简单的二叉树可以组合成复杂的树结构进行复杂的判断，例如下面的更复杂的决策树。为了方便，一般称树上最开始的节点为根节点（root），最末端没有其它分支的节点为叶子节点（leaf），根节点和叶子之间的节点为中间节点（branch）。

创建决策树

创建决策树的过程其实是一个划分输入空间的问题。这个过程可以通过贪心搜索（greedy search）的方法来进行搜索，即在每一个节点的选择时候，每一个变量的每一种可能分割的方法都会被尝试，然后通过一个损失函数来决定什么是当前最优的分割点。对于回归任务，可以使用sum squared error来作为损失函数；对于分类任务，通常使用基尼系数（Gini Index）作为损失函数来衡量这个节点的纯度，流入当前节点的样本的种类越单一，纯度越高。分割决策树的过程可以通过定义最大深度和节点包含的最小样本数来停止递归。

例如我们想给下面一组数据创建决策树，假设对一项疾病的检测我们有2项检测指标以及年龄，希望预测诊断的结果（0或者1）。

	检测1	检测2	年龄	诊断结果
1	T	F	16	1
2	F	T	22	0
3	T	F	17	0
4	T	T	25	1

这里首先试图创建根节点。我们不知道什么是最优的根节点判断条件，这里的策略是对所有可能的判断条件进行尝试，根据基尼系数选择最优的判断条件。首先尝试使用检测1作为判断条件，如果检测1为True，那么诊断结果为1，否则为0。以此为判断可以将4个样本分为左右两个群组，左边群组的诊断结果为1，0，1，右边群组的诊断结果为1，所以仅仅用检测1作为判断条件不能完美地区分诊断结果。类似地，我们可以尝试使用检测2作为判断条件，发现依然不能完美区分诊断结果。当使用年龄作为判断条件的时候，发现年龄一列的数值是整数而不是boolean，这和前两列的数值类型不一样，不过我们可以尝试所有的年龄划分方法，来试图寻找最合适的判断条件。然后通过计算所有分隔结果的基尼系数，选择做优的方法，它们的结果如下图，可以发现使用检测1的结果作为判断条件是作为根节点判断条件的最优选择之一，因此可以选择它作为根节点的判断条件。

这时发现右边的群组已经是一个完美的分隔结果，但是左边仍然是0和1混杂的不纯的结果。但是决策树不是一步就将样本分隔完美，我们可以对左边的群组继续分隔。我们可以尝试使用检测2，以及年龄作为判断条件然后从中选择基尼系数最低的一个，不同判断条件的分隔结果如下，可以发现仍然没有一个条件能够将所有样本完美分隔开，检测2作为判断条件可以将样本分为两个群组，左边群组包含一个1，右边群组包含1和0。

接着对右边的群组使用年龄作为判断条件可以将它们完美分隔开。

可以将构建完成的决策树可视化：

不纯度的度量方法

为了区分一个节点的分隔是否是一次有效的分隔，我们需要一种度量方法进行计算。观察下面三个经过节点分隔后的结果，可以发现：第一个分隔的结果中两边的群组都包含等量的0和1类别，这样的分隔方式是非常不理想的，在术语中被称为不纯的（impure）；第二个分隔的结果中两边的群组分别只包含0或者1，这样的分隔方式是最理想的，也被称为纯度（purity）为1的分隔；第三个分隔结果中，左边包含0和1，右边是完成的1，这样的分隔结果介于完全不纯到纯度为1之间。为了描述分隔的纯度，常用的计算方法包括基尼系数（Gini Index），熵（Entropy），熵的增益（Information Gain）。

基尼系数是用来衡量每个分开的集合的不纯度的指标。基尼系数的计算公式如下，计算过程可以描述为1减去一个群组中每个类别所占比例的平方。基尼系数越高意味着不纯度（Impurity）越高。一个完美的分割可以使得结果的基尼系数为0，一个最差的结果（即对于二分类来说50/50的比例）基尼系数为0.5。

\[\begin{aligned} Gini(P) &= \sum_{k=1}^k P_k (1 - P_k) \\ &= 1 - \sum_{k=1}^k(P_k)^2 \end{aligned}\]

对于上图第一个分隔方案的计算示例如下。对于左边的群组，类别0所占的比例为\(\frac{1}{2}\)，类别1所占的比例为\(\frac{1}{2}\)，使用基尼系数的计算公式可以知道左边群组的基尼系数为\(1 - (\frac{1}{2})^2 - (\frac{1}{2})^2 = 0.5\)；对于右边的群组，类别0所占的比例为\(\frac{1}{2}\)，类别1所占的比例为\(\frac{1}{2}\)，使用基尼系数的计算公式可以知道左边群组的基尼系数为\(1 - (\frac{1}{2})^2 - (\frac{1}{2})^2 = 0.5\)。要描述这个节点分隔的不纯度，需要同时考虑左边群组的不纯度和右边群组的不纯度，由于两个群组的样本个数可能不同，还需要考虑给不同的群组不同的权重，因此这个节点分隔的不纯度可以计算为\(0.5 \times \frac{2}{4} + 0.5 \times \frac{2}{4} = 0.5\)，每个群组的权重都为\(\frac{2}{4}\)。

使用同样的计算方法，我们可以知道第二个分隔的方案的基尼系数计算结果为0，第三个分隔方案的基尼系数计算结果为0.25。使用基尼系数可以来判断一次分隔是否是一次有效地分隔。

熵（Entropy）和熵的增益（Information Gain）也是用来衡量是否得到一个很好的分割节点的指标。它们的计算公式如下：

\[H(S) = - \sum_i p_i(S)\log_2 p_i(S)\] \[IG(S, A) = H(S) - \sum_{v \in Values(A)} \frac{|S_v|}{S}H(S_v)\]

伪代码

FUNC TreeGenerate(dataset):
	IF 如果dataset中全部为同一类C：
		返回叶子节点并标记为C
	ELSE IF 满足递归条件(达到最大深度或者dataset数量小于最小要求)：
		返回叶子节点，标记为dataset中数量较多的标签C
	ELSE：
		从dataset中寻找最佳分割点（使用基尼系数，熵等），得到数据集子集left和right
		返回 Tree(TreeGenerate(left), TreeGenerate(right), 当前分割点条件)	

使用Python实现决策树

banknote 数据集包含1372条记录，每条记录包含5个变量，其中最后一个变量代表这个banknote是否是真的。这是一个典型的二分类问题。

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split

def gini_index(groups, classes):
    """ Calculate the Gini index for a split. Perfect split leads
    gini index to 0.0, the worst split leads to 0.5
    >>> gini_index([[[1, 1], [1, 0]], [[1, 1], [1, 0]]], [0, 1])
    0.5
    >>> gini_index([[[1, 0], [1, 0]], [[1, 1], [1, 1]]], [0, 1])
    0.0
    """
    # count all samples at split point
    n_instances = sum(len(group) for group in groups)
    gini = 0
    for group in groups:
        size = len(group)
        if size == 0:
            continue
        score = 0
        labels =[row[-1] for row in group]
        for c in classes:
            prop = labels.count(c) / size
            score += prop * prop
        gini += (1 - score) * (size / n_instances)
    return gini

def tree(left=None, right=None, is_leaf=False, **kwargs):
    """ Use dict to represent a node on tree """
    if is_leaf:
        return {'left':None, 'right': None, 'label': kwargs['label']}
    elif left is None and right is None:
        return {'left':[], 'right':[], **kwargs}
    else:
        return {'left':left, 'right':right, **kwargs}

def exec_split(index, value, rows):
    """Split dataset based on a feature and a feature value"""
    left, right = [], []
    for row in rows:
        if row[index] >= value:
            right.append(row)
        else:
            left.append(row)
    return [left, right]

def best_split(dataset):
    """ select a best split point for a datast."""
    class_values = list(set(row[-1] for row in dataset))
    best_index, best_value, best_score, best_groups = 999, 999, 999, None
    for index in range(len(dataset[0]) -1):
        for row in dataset:
            groups = exec_split(index, row[index], dataset)
            gini = gini_index(groups, class_values)
            if gini < best_score:
                best_index, best_value, best_score, best_groups = index, row[index], gini, groups
    return best_index, best_value, best_groups


def build_tree(dataset, current_depth=0, max_depth=10, min_size=1):
    """ Build a tree
    """
    if current_depth > max_depth or \
        len(dataset) <= min_size or \
        len(set([row[-1] for row in dataset])) == 1:
            labels = [row[-1] for row in dataset]
            label = max(set(labels), key=labels.count)
            return tree(is_leaf=True, label=label, dataset=dataset)
    else:
        best_index, best_value, best_groups = best_split(dataset)
        left, right = best_groups
        if len(left) == 0:
            labels = [row[-1] for row in right]
            label = max(set(labels), key=labels.count)
            return tree(is_leaf=True, label=label)
        if len(right) == 0:
            labels = [row[-1] for row in left]
            label = max(set(labels), key=labels.count)
            return tree(is_leaf=True, label=label)
        else:
            return tree(
                build_tree(left, current_depth=current_depth+1, max_depth=max_depth, min_size=min_size), 
                build_tree(right, current_depth=current_depth+1, max_depth=max_depth, min_size=min_size), 
                index=best_index, 
                value=best_value
                )

def is_leaf(dtree):
    if dtree['left'] is None and dtree['right'] is None and dtree.get('label', None) is not None:
        return True
    else:
        return False

def predict(dtree, row):
    if is_leaf(dtree):
        return dtree['label']
    elif row[dtree['index']] >= dtree['value']:
        return predict(dtree['right'], row)
    else:
        return predict(dtree['left'], row)

if __name__ == "__main__":
    data = pd.read_csv("./data_banknote_authentication.txt", header=None).values
    trainset, testset = train_test_split(data, random_state=2033)
    dt = build_tree(trainset)
    print("Training done")
    preds = [predict(dt, row) for row in testset]
    acc = sum(pred==row[-1] for pred, row in zip(preds, testset)) / len(testset)
    print("Accuracy: {:.2f}".format(acc))

使用sklearn实现决策树

import numpy as np
import sklearn.datasets as ds
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
import seaborn as sns

# Load dataset and split
X, y = ds.load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2033, test_size=0.33)

# Single Decision Tree
clf = DecisionTreeClassifier(criterion="entropy", min_samples_leaf=3)

# Train phase
dt_clf = clf.fit(X_train, y_train)

# Predict phase
y_hat = dt_clf.predict(X_test)

# Evaluate phase
c = np.count_nonzero(y_hat == y_test)
print("Accuracy: {}/{}={:.2%}".format(c, len(y_test), c / len(y_test)))

print("classification report:")
print(classification_report(y_test, y_hat))

sns.heatmap(
    data=confusion_matrix(y_test, y_hat),
    annot=True,cmap='rainbow',
    linewidths=1.0,
    annot_kws={'size':8},
    yticklabels=['setosa', 'versicolor', 'virginica'],
    xticklabels=['setosa', 'versicolor', 'virginica'],
)
plt.yticks(rotation=0)
plt.show()
plt.savefig("heatmap.svg")

随机森林（Random Forest）

为了提高性能表现，我们可以使用使用许多的不同的树，让多个树的结果投票来决定最终的预测结果。随机森林采用多个方法来保证树存在多样性：

• 对数据集进行随机采样，构建不同的训练数据集 bootstrap dataset；
• 在创建决策树的每一步使用使用随机一部分的特征进行训练，对于分类任务，m 通常取值为 p 的平方根, m 是选择的特征数量，p 是全部特征的数量。

注意到对数据集随机采样或者说bootstrap dataset的时候，会有一定概率有特征没有被选中，这些样本被称为out-of-bag sample，可以使用这些样本作为验证集选择最好的随机特征数量。

为什么随机森林能够提高性能表现？通过每个数随机去掉了一些特征，每个训练后的决策树相互独立，因此平均后的结果减少了模型的variance。

from sklearn.ensemble import RandomForestClassifier

rfc = RandomForestClassifier(n_estimators=100)

# Train phase
rfc.fit(X_train, y_train)

# Evaluate phase
y_hat = rfc.predict(X_test)

c = np.count_nonzero(y_hat == y_test)
print("Accuracy: {}/{}={:.2%}".format(c, len(y_test), c / len(y_test)))

print(confusion_matrix(y_test, y_hat))

print(classification_report(y_test, y_hat))

随机森林超参数的网格搜索

交叉验证和网格搜索的目的是为了寻找最优的超参数。

from sklearn.model_selection import GridSearchCV
# Create the parameter grid based on the results of random search 
param_grid = {
    'bootstrap': [True],
    'max_depth': [80, 90, 100, 110],
    'max_features': [2, 3],
    'min_samples_leaf': [3, 4, 5],
    'min_samples_split': [8, 10, 12],
    'n_estimators': [100, 200, 300, 1000]
}

rfc = RandomForestClassifier()

grid_search = GridSearchCV(estimator = rfc, param_grid = param_grid, 
                          cv = 3, n_jobs = -1, verbose = 2)

# Train phase
grid_search.fit(X_train, y_train)

grid_search.best_params_

best_grid = grid_search.best_estimator_

y_hat = best_grid.predict(X_test)

# Evaluate phase
c = np.count_nonzero(y_hat == y_test)
print("Accuracy: {}/{}={:.2%}".format(c, len(y_test), c / len(y_test)))

print(confusion_matrix(y_test, y_hat))

print(classification_report(y_test, y_hat))

决策树的可视化

决策树的可视化可以使用 graphviz 和 pydot 库来实现。它们都可以通过命令进行安装。

要想安装graphviz，对于 linux 用户:

sudo apt install graphviz

对于 mac 用户:

brew install graphviz

对于 windows 用户:

choco install graphviz

安装pydot包可以使用pip命令：

pip install pydot

from IPython.display import Image
from io import StringIO
from sklearn.tree import export_graphviz
import pydot

feature_names = ['Petal Length', 'Petal Width', 'Sepal Length', 'Sepal Width']
class_names = ['setosa', 'versicolor', 'virginica']

dotfile = StringIO()

export_graphviz(
    dt_clf, # decision tree or singel tree in random forest
    out_file=dotfile,
    feature_names=feature_names, 
    class_names=class_names,
    filled=True,
    rounded=True
)

(graph,) = pydot.graph_from_dot_data(dotfile.getvalue())
# graph.write_png("tree.png") # uncomment this if you want to save the picture
Image(graph.create_png())

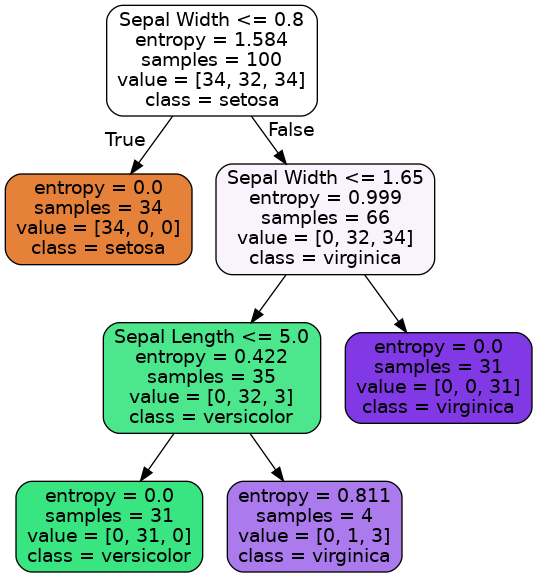
决策树的剪枝

TODO

参考资料

视频

• https://www.youtube.com/watch?v=7VeUPuFGJHk

文档

• Chapter 8 of Introduction to Statistical Learning by Gareth James et al.
• How To Implement The Decision Tree Algorithm From Scratch In Python
• Classification And Regression Trees for Machine Learning
• A Complete Tutorial on Tree Based Modeling from Scratch (in R & Python)
• Hyperparameter Tuning the Random Forest in Python
• How to Implement Random Forest From Scratch in Python
• Enchanted Random Forest

代码

• scikit-learn的决策树实现
• Decision Tree from scratch (not sklearn)