Personalized PageRank
Random Walk
随机游走(Random walk)是指一个物体在某个位置上每次选择一个路径进行移动。
以一个一维坐标轴为例子:

坐标周中心的黑点每次有相同的概率随机移动+1步或者-1步。那么经过1步的移动后,黑点有0.5的概率在1位置,0.5的概率在-1位置;经过2步移动后,黑点有0.5概率在0位置,0.25概率在2位置,0.25概率在-2位子…这个概率并不是说黑点一定移动到某个位置,而是在很多次重复试验后,黑点移动到每个位置的数量会趋近于这个分布。
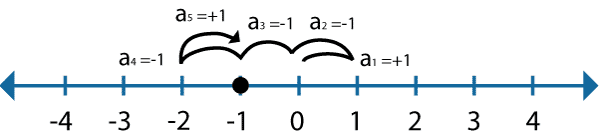
同时还可以发现,在这种情况下,经过奇数次的移动后,黑点永远不会出现在0,2,-2这样的偶数位置点;同样经过偶数次移动后,黑点永远不会出现在-1,1这样的奇数位置的点。
下面的视频很好的解释了一维坐标轴上的随机游走,并展示了随着不同的游走步数产生的不同的黑点落点位置的分布:
我们可以将1维坐标轴上的随机游走推广到更多的情况中,比如二维,三维的情况,比如在一个graph上的情况.
例如在下面的一个图中,红色位置的节点有一段信息,将在graph上传播,这个传播的过程可以用随机游走来模拟。最简单的情况可以是一个节点的信息会以相同的概率传播到相邻接的节点。在下面的例子中,红色节点只包含一个邻居,因此在第一步的时候只会把全部的信息传播到邻居节点,这是最简单的情况;但是随着步数增长,信息会逐渐传播到每个节点上,并且连接邻居多多节点会保持更高多信息量,这个剩余信息量可以用来对每个节点进行排序,这就是PageRank算法对基本思想。
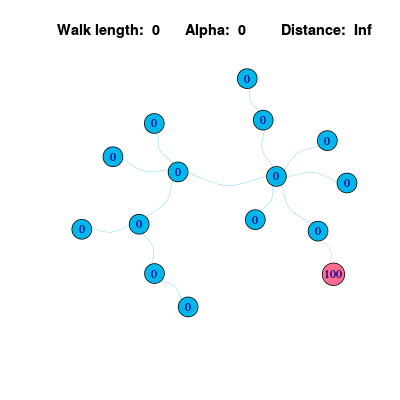
这里可以用数学方法来表达信息传播对过程,假设一个graph有一个\(N\)个节点,那么节点上的信息值可以初始化为\(\mathbf{x} = \left[\matrix{1 \\ 0 \\ \vdots\\ 0}\right] \in \mathbb{R}^N\),这个graph可以用邻接矩阵矩阵表示为\(A \in \mathbb{R}^{N \times N}\),同时需要将邻接矩阵的每一行归一化成和为1。那么每一步信息传播可以表示为:
\[\mathbf{x^k} = A \mathbf{x^{k-1}}\]对于每一个节点来说,这个计算过程可以表示为:
\[P V(u)=\sum_{v \in \mathcal{N}(u)} P V(v)\]其中\(u\)表示当前节点,\(\mathcal{N}(u)\)表示当前节点的所有邻居。这两种写法表示的计算过程是相同的,区别在于后者更适合于目前的图网络计算框架(比如DGL, PyG),而前者的向量化计算会因为避免了循环更加高效。
Lazy Random Walk
但是上面的算法仍然存在一些问题,通过可视化信息传播过程,可以发现各个节点上的信息值不停波动,不会趋于稳定。这是因为在一个下面的图是一个二分图,二分图存在两组节点使得组内节点互相不连接,这就导致了信息最终在两个节点组之间不停波动。上述的一维坐标上的随机游走也存在一样的问题,最后的黑点位置的分布在奇数点和偶数点之间波动,而不是趋于稳定。
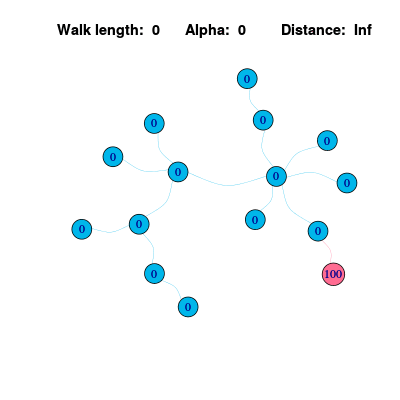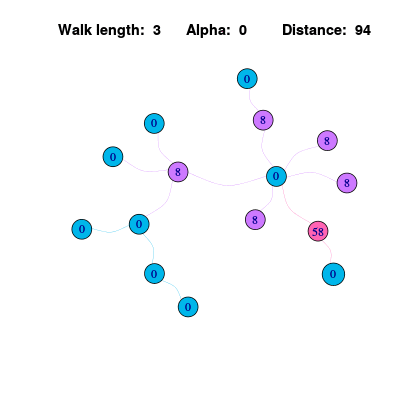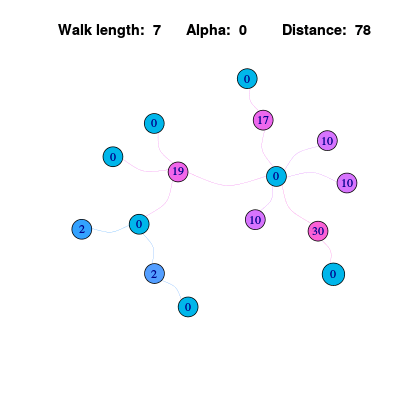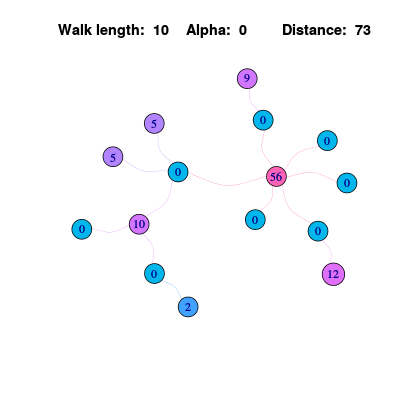
解决这个问题的一个方法是使得传播的信息更“懒”一些,即每次节点只会传播出去1/2的信息,另外1/2会保留。这个计算方法用公式可以表示为:
\[\mathbf{x^{k}} = \frac{1}{2}(A + I)\mathbf{x^{k-1}}\]同样给出每个节点的计算公式:
\[P V(u)=\frac{1}{2}(u + \sum_{v \in \mathcal{N}(u)} P V(v))\]这时可以随着步数的迭代,信息的传播趋于稳定,这是我们希望看到的。
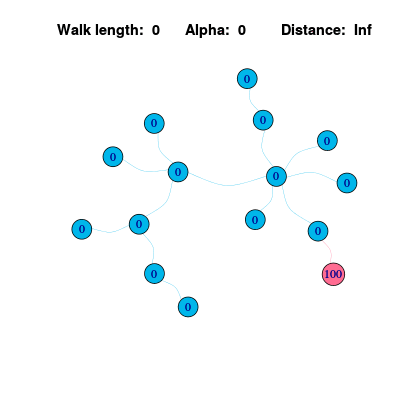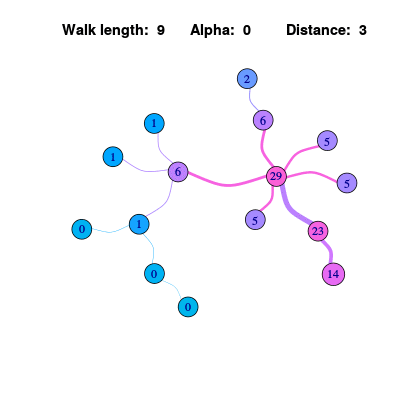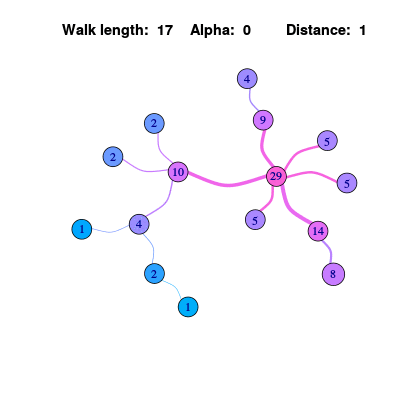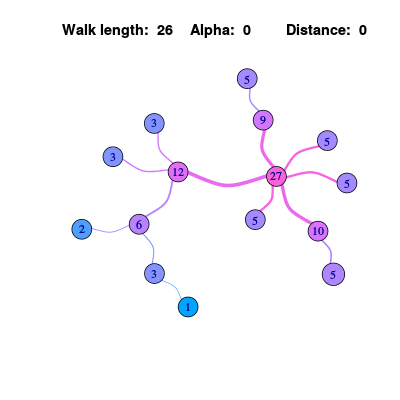
Personalized Page Rank
在上面的算法中,除了各个节点的信息值趋于稳定外,同时会发现作为信息源的节点会逐渐变得不明显。如果可以在最终的结果中让信息源节点保留更多的权重,和信息源直接关联的节点取得更高的排序,那么这个排序结果就可以称为是个性化的(因为不同的信息源会产生不同的排序)。
为了实现这个目标,可以进一步将传播公式修改为:
\[\mathbf{x^{k}} = (1-\alpha)*A\mathbf{x^{k-1}} + \alpha * E\] \[P V(u)= (1-\alpha)*\sum_{v \in \mathcal{N}(u)} P V(v) + \alpha * e\]其中\(\alpha\)是一个0到1到常数,\(E\)是一个向量用来表示源信息,如果源信息只从一个节点出发,那么就是其它的节点都是0,只有那个节点包含常数。可以发现作为信息源的0号节点和相关节点始终保持较高的排序。
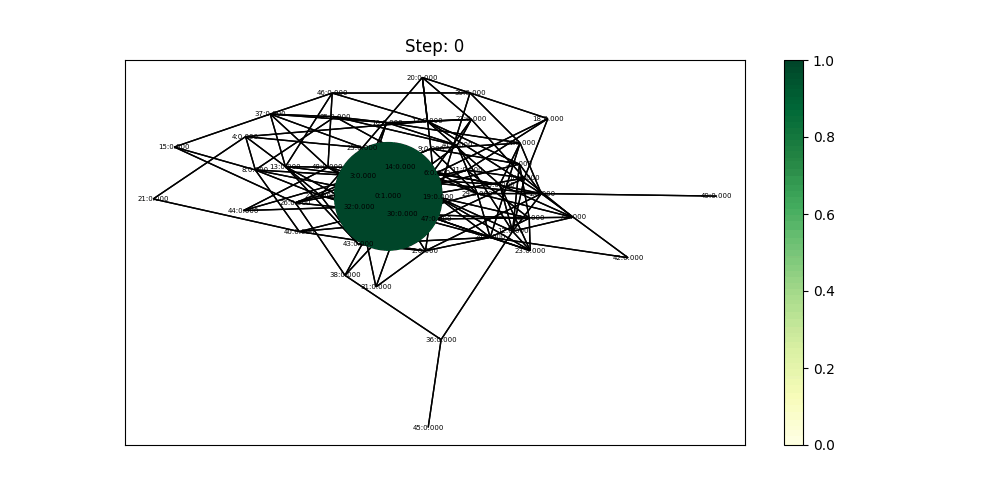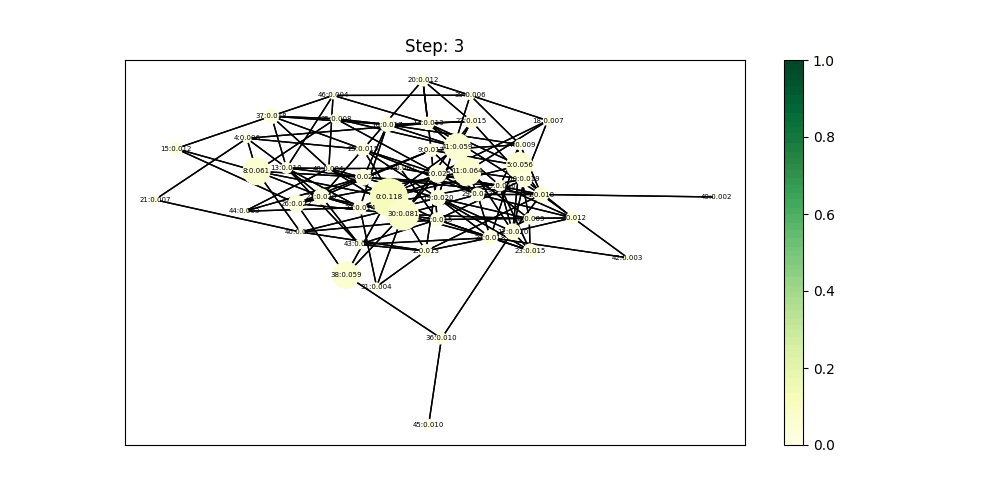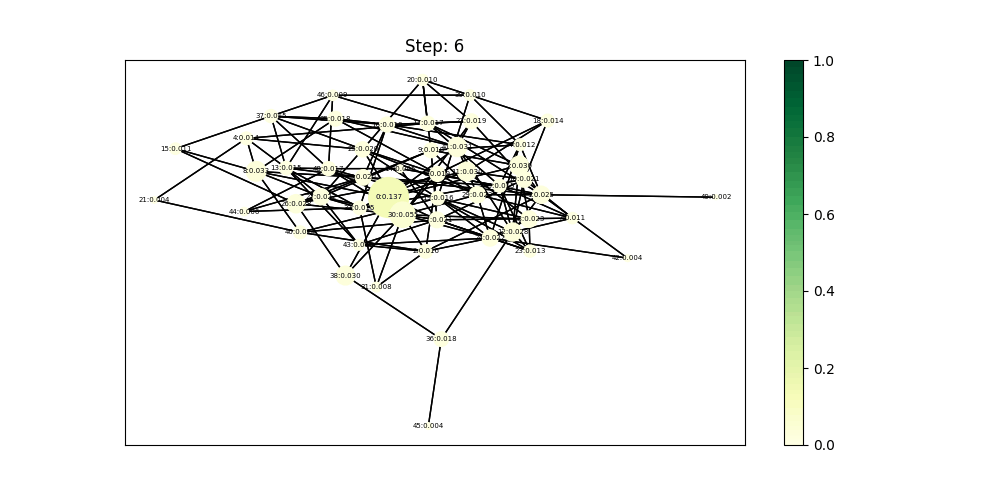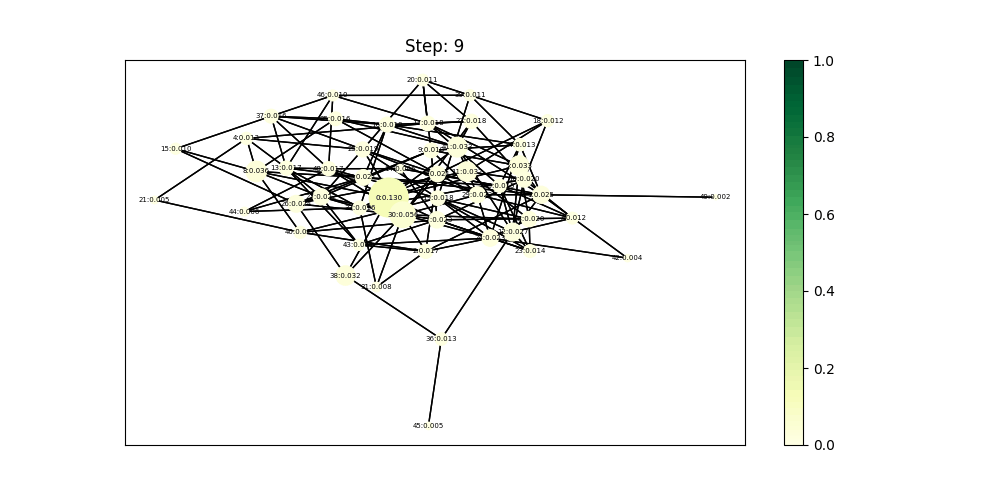
ppagerank使用dgl库的实现代码示例如下:
import networkx as nx
import matplotlib.pyplot as plt
import torch
import dgl
N = 50 # number of nodes
DAMP = 0.85 # damping factor
K = 10 # number of iterations
SEED = 9
ALPHA = 0.1
g = nx.nx.erdos_renyi_graph(N, 0.1, seed=SEED)
g = dgl.DGLGraph(g)
g.ndata['pv'] = torch.zeros(N)
g.ndata['pv'][0] = 1
g.ndata['e'] = g.ndata['pv'].clone()
g.ndata['deg'] = g.out_degrees(g.nodes()).float()
# DGL original version
# g.ndata['pv'] = torch.ones(N) / N
# def pagerank_message_func(edges):
# return {'pv' : edges.src['pv'] / edges.src['deg']}
# def pagerank_reduce_func(nodes):
# msgs = torch.sum(nodes.mailbox['pv'], dim=1)
# pv = (1 - DAMP) / N + DAMP * msgs
# return {'pv' : pv}
# Naive random walk
# def pagerank_message_func(edges):
# return {'pv' : edges.src['pv'] / edges.src['deg']}
# def pagerank_reduce_func(nodes):
# msgs = torch.sum(nodes.mailbox['pv'], dim=1)
# pv = msgs
# return {'pv' : pv}
# Lazy random walk
# def pagerank_message_func(edges):
# return {'pv' : edges.src['pv'] / edges.src['deg']}
# def pagerank_reduce_func(nodes):
# msgs = torch.sum(nodes.mailbox['pv'], dim=1)
# pv = 0.5*(nodes.data['pv'] + msgs)
# return {'pv' : pv}
# Personalized Page Rank
def pagerank_message_func(edges):
return {'pv' : edges.src['pv'] / edges.src['deg']}
def pagerank_reduce_func(nodes):
msgs = torch.sum(nodes.mailbox['pv'], dim=1)
pv = (1-ALPHA)*msgs + ALPHA*nodes.data['e']
return {'pv' : pv}
g.register_message_func(pagerank_message_func)
g.register_reduce_func(pagerank_reduce_func)
def pagerank_naive(g):
# Phase #1: send out messages along all edges.
for u, v in zip(*g.edges()):
g.send((u, v))
# Phase #2: receive messages to compute new PageRank values.
for v in g.nodes():
g.recv(v)
for k in range(K):
print(g.ndata['pv'])
pagerank_naive(g)
pos=nx.spring_layout(g.to_networkx(), seed=SEED)
colors = g.ndata['pv']
nc = nx.draw_networkx_nodes(g.to_networkx(), pos,
node_size=g.ndata['pv']*6000, node_color=g.ndata['pv'], cmap=plt.cm.coolwarm)
plt.colorbar(nc)
labels = {}
for node, pv in zip(g.to_networkx().nodes(), g.ndata['pv']):
labels[node] = "{}:{:.3f}".format(node, pv)
lc = nx.draw_networkx_labels(g.to_networkx(), pos,
labels=labels, font_size=5)
ec = nx.draw_networkx_edges(g.to_networkx(), pos,
arrows=False, aplha=0.2)
plt.show()
作为参考,这里列出DGL官方教程中使用的PageRank算法:
\[\mathbf{x}^{k}=\frac{1-d}{N} \mathbf{1}+d \mathbf{A} * \mathbf{x}^{k-1}\] \[P V(u)=\frac{1-d}{N}+d \times \sum_{v \in \mathcal{N}(u)} \frac{P V(v)}{D(v)}\]