牛顿法(Newton's Method)
前言
牛顿法是一个迭代优化算法:它可以对任意可以微分的函数的0处进行估计。可微分的函数在每一个点都有一个近似的直线,牛顿法根据这些直线估计来寻找函数取0的时候的值。
方法
想象有一条直线穿过一点$(x, f(x))$,并且在这点和函数$f(x)$的曲线有相同的斜率。这样的线就叫tangent,这个斜率也被成为$f$在$x$的导数。
这条线的斜率是对于函数参数的变化,函数值变化的变化率。因此,将$x$平移一段等于$f(x)$除以斜率的距离会得到tangent斜线与0相交的那个点的参数值。
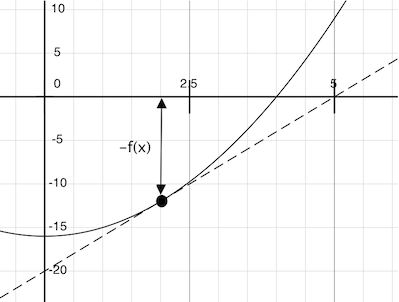
这里newton_update表达了跟随tangent line将$x$平移到0的计算过程,这里的df是f的导数。
def newton_update(f, df):
def update(x):
return x - f(x) / df(x)
return update
然后关于newton_update定义了find_root函数,我们的improve算法,和对比$f(x)$是否接近与0。
def find_zero(f, df):
def near_zero(x):
return approx_eq(f(x), 0)
return improve(newton_update(f, df), near_zero)
最后应用一个优化迭代的框架,可以得到
def improve(update, close, guess=1):
while not close(guess):
guess = update(guess)
return guess
def approx_eq(x, y, tolerance=1e-3):
return abs(x - y) < tolerance
def newton_update(f, df):
def update(x):
return x - f(x) / df(x)
return update
def find_zero(f, df):
def near_zero(x):
return approx_eq(f(x), 0)
return improve(newton_update(f, df), near_zero)
def square_root_newton(a):
def f(x):
return x*x - a
def df(x):
return 2 * x
return find_zero(f, df)
print(square_root_newton(4))
# 2.0000000929222947