奇异值分解(SVD)
前言
SVD,Singular Value Decomposition有着非常广泛的用途。图片降噪,压缩,PCA, 电影或者商品推荐(Collaborative Filtering)都是它的应用场景。如此强大的一个工具,让我们一起掌握它!
SVD
什么是SVD?SVD是说任意一个矩阵都可以分为3个部分。\(U \Sigma V^T\)。其中\(U\)是一个正交矩阵,\(\Sigma\)是一个对角矩阵,\(V^T\)也是一个正交矩阵。从物理意义上来说就是旋转,拉伸,旋转。
那么如何得到\(U\),\(\Sigma\),\(V\)这三个部分?
那么,我们让一个矩阵\(A\)做奇异值分解,那么我们有:
\[A = U \Sigma V^T\]我们先来计算\(V\),首先计算\(A\)和它的转置的乘积:
\[A^TA = (V \Sigma^T U^T) U \Sigma V^T = V(\Sigma^T \Sigma) V\]\(A\)矩阵两个维度不一定一样,但是\(A^TA\)维度是一样的,而且是一个半正定矩阵,所以它的特征值矩阵是正交矩阵。中间的\((\Sigma^T \Sigma)\)是矩阵\(A\)的\(\sigma^2\)。
然后我们继续去计算\(U\),方法很简单,计算:
\[AA^T = (U \Sigma V^T) V \Sigma^T U^T = U(\Sigma \Sigma^T) U^T\]通过计算\(AA^T\)的特征矩阵我们就可以得到\(U\)。
下面来看一个具体的例子:
如果有:\(A = \left[\begin{matrix} 2 & 2 \\ 1 & 1 \end{matrix}\right]\) 如何计算它的奇异值分解?
使用numpy的linalg包可以直接计算出\(A\)的奇异值分解:
import numpy as np
A = np.array([[2, 2], [1, 1]])
U, S, V = np.linalg.svd(A)
print(S)
# [3.16227766e+00 1.10062118e-17]
更为精确的就是:
\[A = \left[\begin{matrix} 2 & 2 \\ 1 & 1 \end{matrix}\right] = \left[\begin{matrix} \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}} \\ \frac{-1}{\sqrt5} & \frac{2}{\sqrt{5}} \end{matrix}\right] \left[\begin{matrix} \sqrt{10} & \\ & 0 \end{matrix}\right] \left[\begin{matrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{-1}{\sqrt{2}} \end{matrix}\right]\]或者,我们可以分步计算来进一步了解这个过程:
import numpy as np
A = np.array([[2, 2], [1, 1]])
W, V = np.linalg.eig(A.dot(A.T))
S = np.sqrt(W)
_, U = np.linalg.eig(A.T.dot(A))
print(S)
# [3.16227766 0. ]
应用
图像去噪
我们可以通过SVD分解,得到一些奇异值,然后选择较大的几个奇异值对原来的矩阵进行还原:
\[A = U S V^T = \sigma_1 \vec{u_1} \vec{v_1}^T + \sigma_2 \vec{u_2} \vec{v_2}^T + \cdots = \sum \sigma_i \vec{u_i} \vec{v_i}^T\]这可以帮助我们抛弃影响图像中影响较小的部分,而这些部分很可能就是噪声。(公式中\(u\)按列索引,\(v\)按行索引)
from numpy import array
import numpy as np
import seaborn as sns
A = \
array([[0., 0., 0., 0., 0., 0., 0.],
[0., 1., 1., 1., 1., 1., 0.],
[0., 1., 1., 1., 1., 1., 0.],
[0., 1., 1., 0., 1., 1., 0.],
[0., 1., 1., 0., 1., 1., 0.],
[0., 1., 1., 0., 1., 1., 0.],
[0., 1., 1., 0., 1., 1., 0.],
[0., 1., 1., 1., 1., 1., 0.],
[0., 1., 1., 1., 1., 1., 0.],
[0., 0., 0., 0., 0., 0., 0.]])
sns.heatmap(A); plt.show() # It's a clean image
noise = np.random.rand(*A.shape) / 5
noised = A + noise
sns.heatmap(noised); plt.show() # It's a noised image
# Then use svd to only select first 2 components
u, s, v = np.linalg.svd(noised)
recovered = np.zeros_like(A)
for i in range(2):
recovered += np.dot(u[:, i].reshape(10, 1), v[i].reshape(1, 7))*s[i]
sns.heatmap(recovered); plt.show() # It's a denoised image
下面的过程可以帮助进一步理解SVD的分解和还原:

PCA
对矩阵进行SVD分解后得到的奇异值代表着每个元素的影响,我们可以利用奇异值大小来排序各个元素的重要性。这就是所说的主成分分析(PCA)。
>>> data = [[-1,-1,0,2,1],[2,0,0,-1,-1],[2,0,1,1,0]]
>>> data = np.array(data)
>>> data
# array([[-1, -1, 0, 2, 1],
# [ 2, 0, 0, -1, -1],
# [ 2, 0, 1, 1, 0]])
>>> U, S, VT = np.linalg.svd(data - data.mean(0))
... data_pca = np.dot(data - data.mean(0), VT[:2].T)
... print(data_pca)
>>> data_pca.dot(VT[:2]) + data.mean(0) # 恢复数据
# 和sklearn中PCA的结果对比
>>> from sklearn.decomposition import PCA
... pca = PCA(n_components=2)
... data_pca = pca.fit_transform(data)
... print(data_pca)
>>> data_pca.dot(pca.components_) + (pca.mean_) # 恢复数据
Collaborative Filtering
Collaborative Filtering或者简称CF,它将用户评价矩阵通过矩阵分解(Matrix Factorization)的方法分解为用户特征和商品特征两个部分。将用户特征与商品矩阵相乘还原出的矩阵可以填补用户评价矩阵中缺失的部分。
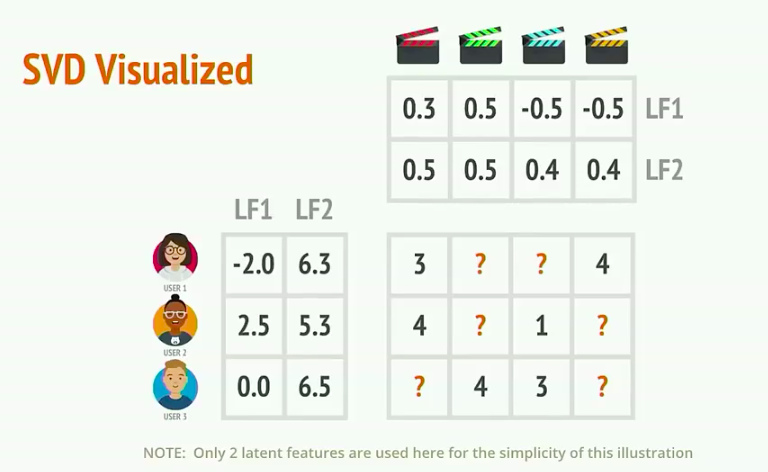
你可以使用Surprise包来通过6行代码快速了解SVD如何应用于推荐系统。