Recursive

Recursive

一个函数如果在主体部分调用自身，那么这个函数就被称为递归函数。 首先从一个简单的问题开始，编写一个方程来计算一个自然数每一个位数的和：

def sum_digit(n):
    if n < 10:
        return n
    else:
        all_but_last, last = x // 10, x % 10
        return last + sum_digit(all_but_last)

sum_digit(1234) # 10

递归的思想是把复杂的问题拆分为一个简单的情况（base case）和分解复杂问题的方法 （recursive condition）。如果我们的目的是计算自然数每一位数字之和，最简单的情况是该自然数只有一位，这时只要返回该数字本身。而对于更加复杂的情况，分解该问题的方法是将多位数字分解位all_but_last和last两个部分，然后使用加法连接两部分的结果。我们相信sum_digit(all_but_last)会给出最终要想的结果。这时问题的范围已经缩小了一位。

作为模板，递归函数通常都会包含基线情况（base case）和递归情况（recursive case），在这里base case是n < 10，这是简单的情况。此外还需要分解复杂的问题到简单的问题，这里一个数字被分解为all_but_last和last。被分解后的问题的解决方法和原来的方法一样，比如这里对于n和all_but_last，计算它们各位之和的方法是一样的，所以对分解后的问题调用原来的方法。最后需要连接每个分解后的问题的结果，这里只需要加起来就可以了。

Mutual Recursion

当一个递归过程是由两个函数互相调用对方实现的，那么这些函数就称为mutually recursive。例如，考虑如下定义奇数和偶数：

• 如果比一个奇数大1，那么这个数字是偶数。
• 如果比一个偶数大1，那么这个数字是奇数。
• 0是偶数。 根据这个定义，可以实现这样的相互递归调用来判断一个数字的奇偶： ```python def is_even(n): if n == 0: return True else: return is_odd(n-1)

def is_odd(n): if n == 0: return False else: return is_even(n-1)

result = is_even(4)

## Printing in Recursive Functions
一条statement既可以放在recursive部分的前面，也可以放在recursive部分的后面。
```python
def cascade(n):
    if n < 10:
        print(n)
    else:
        print(n)
        cascade(n//10)
        print(n)

>>> cascade(2013)
2013
201
20
2
20
201
2013

那么如果打印出相反的cascade呢？像这样：

>>> inverse_cascade(2013)
2
20
201
2013
201
20
2

这里有一个方法，需要定义两个相反的函数grow和shrink：

def inverse_cascade(n):
    grow(n)
    print(n)
    shrink(n)

def f_then_g(f, g, n):
    if n:
        f(n)
        g(n)

grow = lambda n: f_then_g(grow, print, n//10)
shrink = lambda n: f_then_g(print, shrink, n//10)

Tree recursion

另一个常用的计算模板是树形递归，它的特点是在一次函数中多次调用自己。最简单的例子是Fibonacci数列的递归实现：

def fib(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fib(n-1) + fib(n-2)

这里在一次调用fib函数的过程中，调用了fib(n-1)和fib(n-2)两次。

递归和循环的实现有时候可以互相转换，但是有的问题用tree recursion是最好的方法，没有之一。这里给一个例子：

Partitions：对于一个正整数n，使用最大为m的整数来分解它，可能的分解方法的数量成为它的partition。例如，对于整数6，使用最大为4的整数来分解它，一共9种分法：
6 = 2 + 4
6 = 1 + 1 + 4
6 = 3 + 3
6 = 1 + 2 + 3
6 = 1 + 1 + 1 + 3
6 = 2 + 2 + 2
6 = 1 + 1 + 2 + 2
6 = 1 + 1 + 1 + 1 + 2
6 = 1 + 1 + 1 + 1 + 1 + 1

我们希望定义一个函数count_partitions(n, m)，输入整数n和最大分解的部分m，得到它的分解方法数量。

对于这个问题，先做如下观察：

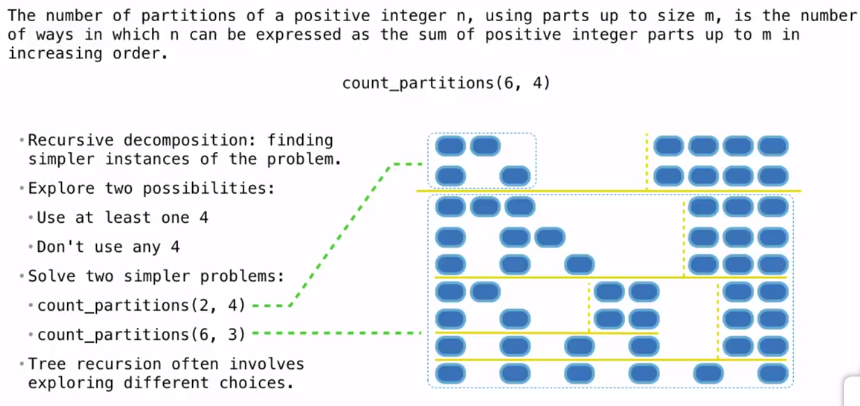
发现规律如下：对于n=6的情况，分解方法可以分为包含4和不包含4两个部分，可以使用这个规律将该问题分解为更小的问题。具体来说，对于整数6，最大整数为4的分解方法可以分为：

• 不包含4的部分：等于整数6-4=2，最大为4的partitions
• 包含4的部分: 等于整数6，最大为3的partitions

对于base case，可以这样设定：

• 如果n为0，只有1种partition
• 如果小于0，有0种partition
• 如果m等于0，有0中partition 最终实现如下：

  >>> def count_partitions(n, m):
        """Count the ways to partition n using parts up to m."""
        if n == 0:
            return 1
        elif n < 0:
            return 0
        elif m == 0:
            return 0
        else:
            return count_partitions(n-m, m) + count_partitions(n, m-1)
  >>> count_partitions(6, 4)
  9
  >>> count_partitions(5, 5)
  7
  >>> count_partitions(10, 10)
  42
  >>> count_partitions(15, 15)
  176
  >>> count_partitions(20, 20)
  627
  

参考资料

• Recursive Functions
• [算法图解]